RECTA DEGRESION POR EL METODO DE LOS MINIMOS CUADRADOS

RECTA DEGRESION POR EL METODO DE LOS MINIMOS CUADRADOS

Cuando la nube de puntos adopta una forma definida, se pueden aproximar sus puntos mediante una línea curva en general, que llamamos curva de regresión.

Nos centraremos entonces en calcular la ecuación de una recta que "mejor se adapte" a una nube de puntos dada. En los ejemplos anteriores lo hemos hecho a ojo, ahora lo haremos con un criterio más preciso.

Para ello existen varios métodos, siendo el más utilizado el de los mínimos cuadrados. Consiste en hacer mínima la suma de los cuadrados de las diferencias entre los valores experimentales y los obtenidos mediante la recta. Por lo tanto, si consideramos la Y=aX+b, mediríamos lo bien (o mal) que se ajusta a nuestros puntos por medio de la cantidad.

¿En qué consiste?

Sea la muestra observada de valores del par de variables (X, Y):

(x₁, y₁), (x₂, y₂), (x₃, y₃), ..., (x_n, y_n)

Se trata de obtener los valores a y b de manera que se minimice la función:

 

La solución es la siguiente:

 

 

Sustituyendo los valores a y b anteriores, tenemos la recta:

y = a + bx

 que es conocida como la recta de regresión Y/X.

Ejemplo: Para el ejemplo de Pesos (kgs.) - Estaturas (cms.) Peso en Kgs. 60 65 70 70 68 50 60 Altura en cms. 167 170 170 180 170 155 160 Frecuencias (ni) 1 5 2 4 2 1 1 y - y = 1.11(x-x ) atan (1.11) = 47,89 º

COEFICIENTE DE CORRELACION "r" DE PEARSON

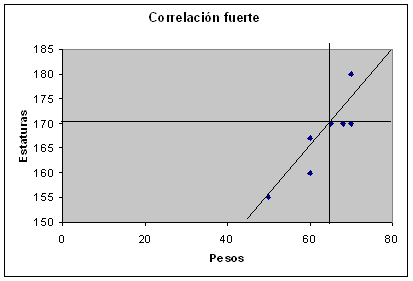
CORRELACION LINEAL:

Mide el grado de intensidad de esta posible relación entre las variables. Este coeficiente se aplica cuando la relación que puede existir entre las varables es lineal (es decir, si representaramos en un gáfico los pares de valores de las dos variables la nube de puntos se aproximaría a una recta).

No obstante, puede que exista una relación que no sea lineal, sino exponencial, parabólica, etc. En estos casos, el coeficiente de correlación lineal mediría mal la intensidad de la relación las variables, por lo que convendría utilizar otro tipo de coeficiente mas apropiado.

Para ver, por tanto, si se puede utilizar el coeficiente de correlación lineal, lo mejor es representar los pares de valores en un gráfico y ver que forma describen.

El  se calcula aplicando la siguiente fórmula:

Es decir:

se denomina  y se calcula de la siguiente manera: en cada par de valores (x,y) se multiplica la "x" menos su media, por la "y" menos su media. Se suma el resultado obtenido de todos los pares de valores y este resultado se divide por el tamaño de la muestra.

 se calcula el produto de las varianzas de "x" y de "y", y a este produto se le calcula la raíz cuadrada.

Ejemplo:

 vamos a calcular el coeficiente de correlación de la siguiente serie de datos de altura y peso de los alumnos de una clase:

Alumno	Estatura	Peso	Alumno	Estatura	Peso	Alumno	Estatura	Peso
x	x	x	x	x	x	x	x	x
Alumno 1	1,25	32	Alumno 11	1,25	33	Alumno 21	1,25	33
Alumno 2	1,28	33	Alumno 12	1,28	35	Alumno 22	1,28	34
Alumno 3	1,27	34	Alumno 13	1,27	34	Alumno 23	1,27	34
Alumno 4	1,21	30	Alumno 14	1,21	30	Alumno 24	1,21	31
Alumno 5	1,22	32	Alumno 15	1,22	33	Alumno 25	1,22	32
Alumno 6	1,29	35	Alumno 16	1,29	34	Alumno 26	1,29	34
Alumno 7	1,30	34	Alumno 17	1,30	35	Alumno 27	1,30	34
Alumno 8	1,24	32	Alumno 18	1,24	32	Alumno 28	1,24	31
Alumno 9	1,27	32	Alumno 19	1,27	33	Alumno 29	1,27	35
Alumno 10	1,29	35	Alumno 20	1,29	33	Alumno 30	1,29	34

Aplicamos la fórmula:

	(1/30) * (0,826)
r =	----------------------------------------------------------
	(((1/30)*(0,02568)) * ((1/30)*(51,366)))^(1/2)

 

 

r =	0,719
x	x

Por lo tanto, la correlación existente entre estas dos variables es elevada (0,7) y de signo posítivo.